07 - Tuesday

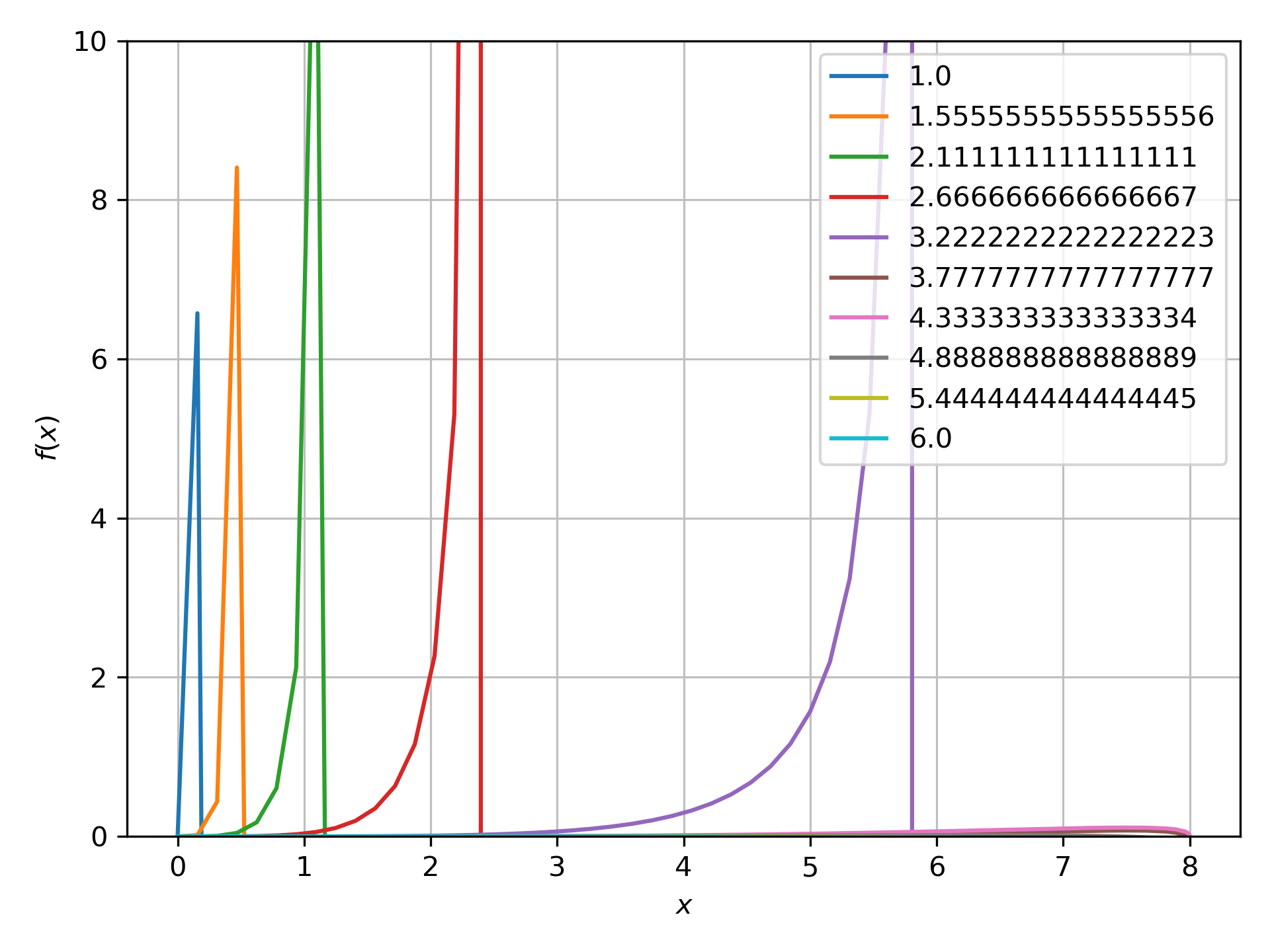
On closer inspection of the plots, it seems the errors are actually spiking at the point the null geodesics terminate at the \(r=0\) singularity. 

The time dependent metric in (1D) Schwarzschild coordinates is:

\[\mathrm{d}s^2=-\left(1-\frac{2(m_0^3-t)^{\frac{1}{3}}}{r}\right)\mathrm{d}t^2+\left(1-\frac{2(m_0^3-t)^{\frac{1}{3}}}{r}\right)^{-1}\mathrm{d}r^2\]

So:

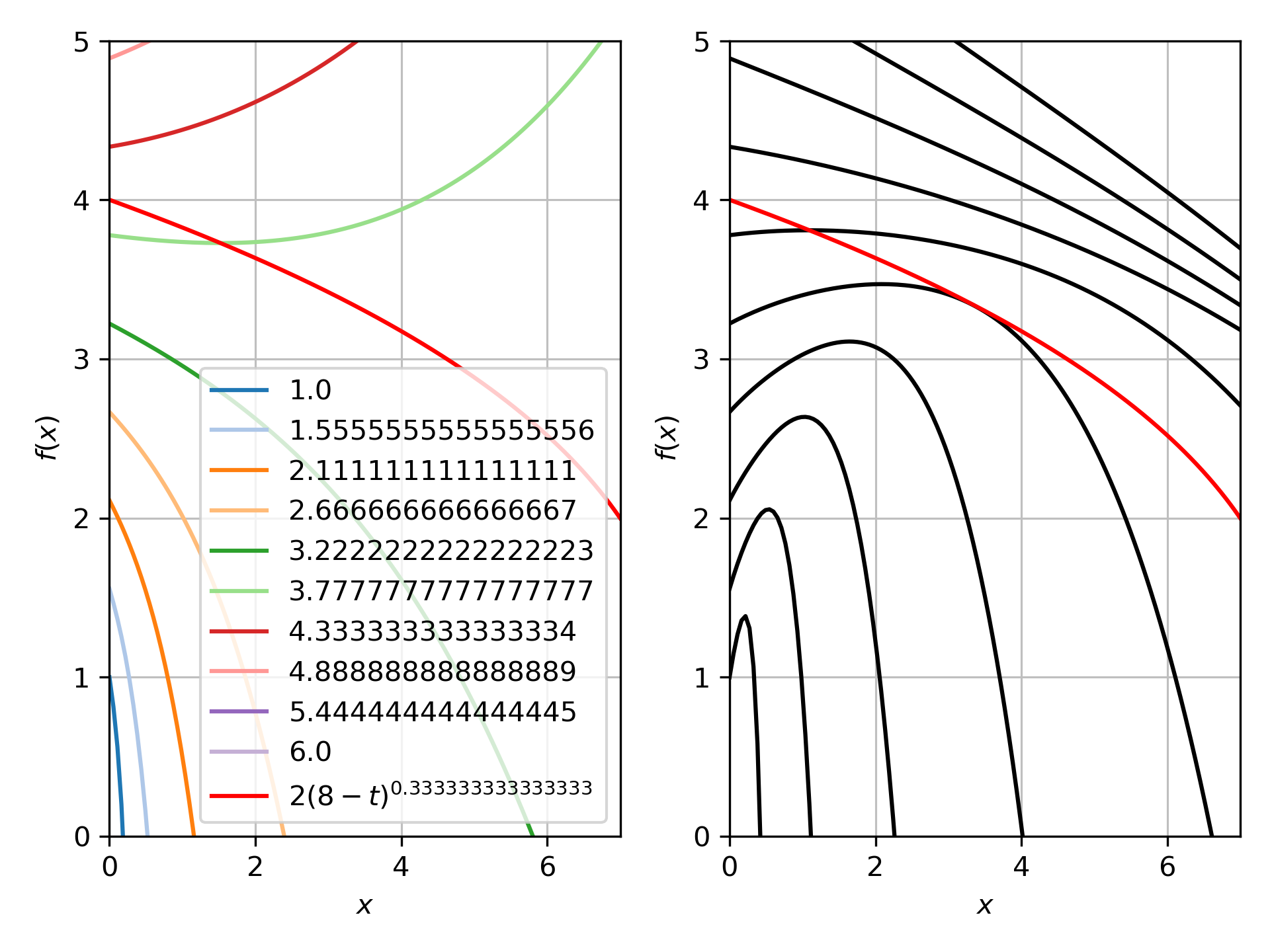
\[r=2(m_0^3-t)^{\frac{1}{3}}\]\[\mathrm{d}s^2=0\]

Which is still true for photons, however, the event horizon then moves past the photon, so the null geodesic is no longer at it and it can continue moving. If that's the case, it should be impossible to find a ray which falls from outside \(r=r_s\) and ends up inside the event horizon. 

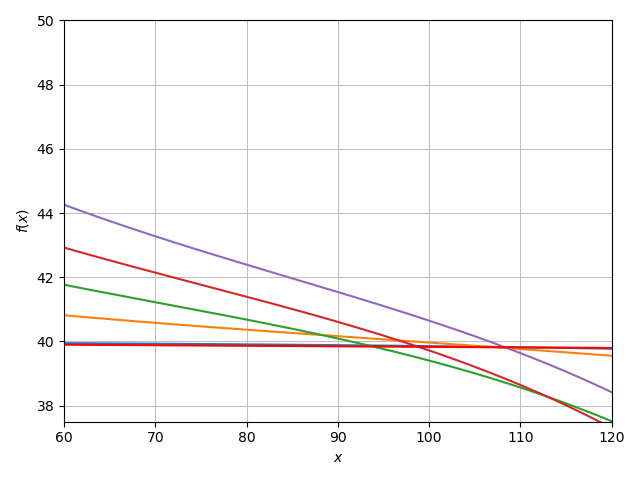
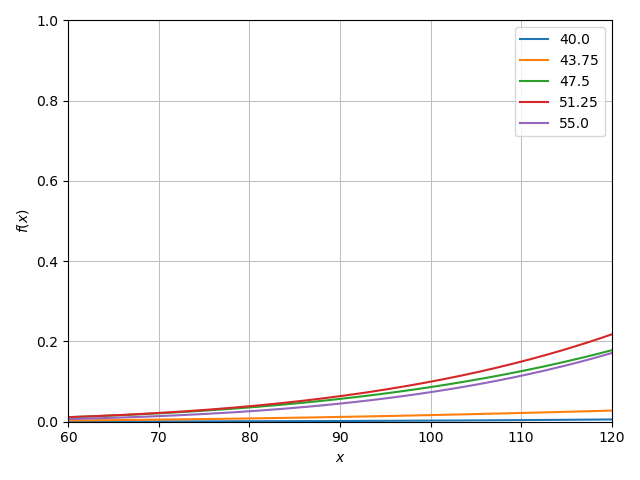
We see in the above that the infalling rays actually can cross (\(m_0=20\)), but this is probably because the series solution has a small error that has accumulated at this point. Finding the series around the time of crossing \(t\approx93.5\) :

I wasn't able to do this in the end, I suspect there is an open issue with sympy, so I may need to fix it myself and replace my copy of sympy with my fix as I don't expect that a PR will be merged in a timely fashion. I might also just test this in mathematica or something…

 

It might also be worth thinking about the fact that photons only normally reach the event horizon after infinite time, so for an extremely large initial mass (because we have all constants=1), it should take a large amount of time. We could compare the derivative of the geodesic as it approaches the event horizon, it should still be tending to 1.