08 - Wednesday

I reran a lot of the plots using 6th and 7th order power series, while they do seem to have some paths that act more sensibly, there are others which act even worse. Such as a trajectory which escapes before falling back below the collapsing horizon…

The trajectories shouldn't leave and then fall back in. Null geodesics shouldn't change direction without crossing the event horizon

Some higher order power series, they look a little better but still approach and pass the horizon even with a large mass m_0=20

some errors for the above, not great really

Some trajectories and the derivatives given by substitution into the ODE, and their actual derivatives

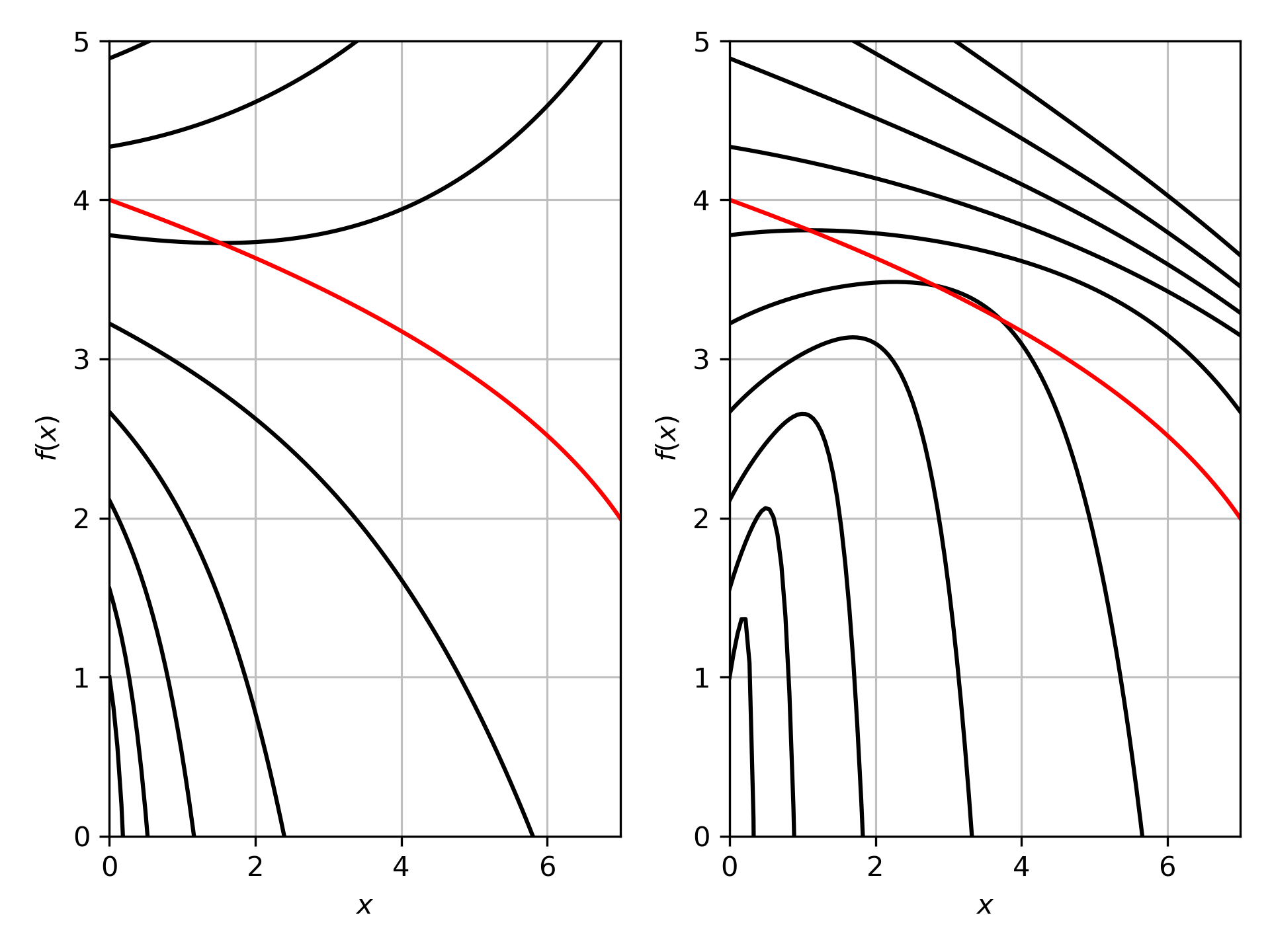
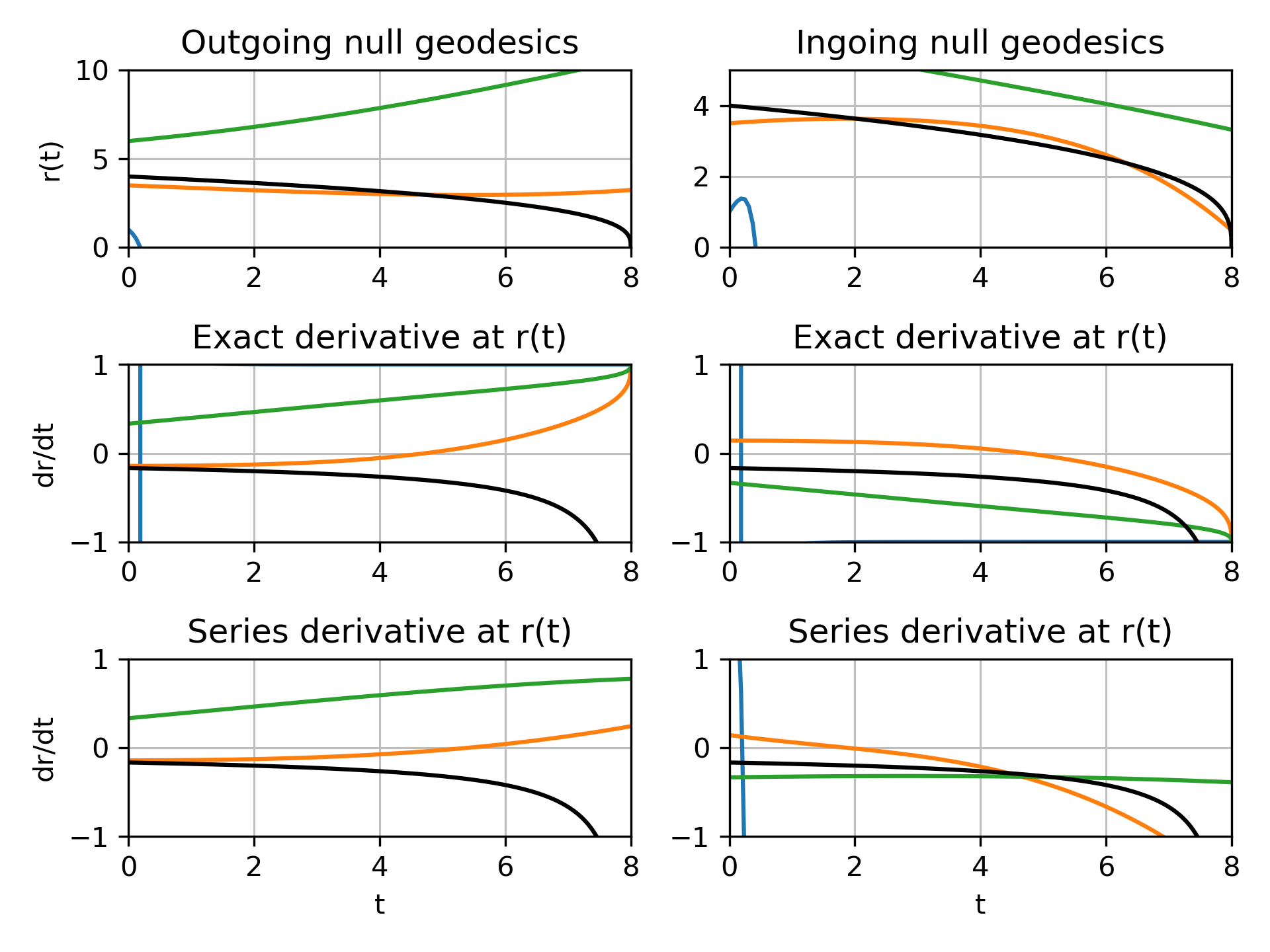
As can be seen in this image, the orange ray should always have a gradient greater than that of the Schwarzschild radius, but the power series isn't obeying this at all.

This suggests that a much better approach would be to numerically solve for the rays rather than getting a series. I haven't been able to find a way to do this in sympy, but thankfully I'm very experienced with it.

It turns out it's fairly easy to do, you just lambdify the ODE, then use scipy to numerically integrate it.

It also turns out that the scipy integrator is very slow, numbalsoda is a C++ implementation of LSODA which should be much nicer to work with. My docker image doesn't have numbalsoda so I need to rebuild it.

Numerical solutions. Some trajectories terminate early due to limitations in the solver.

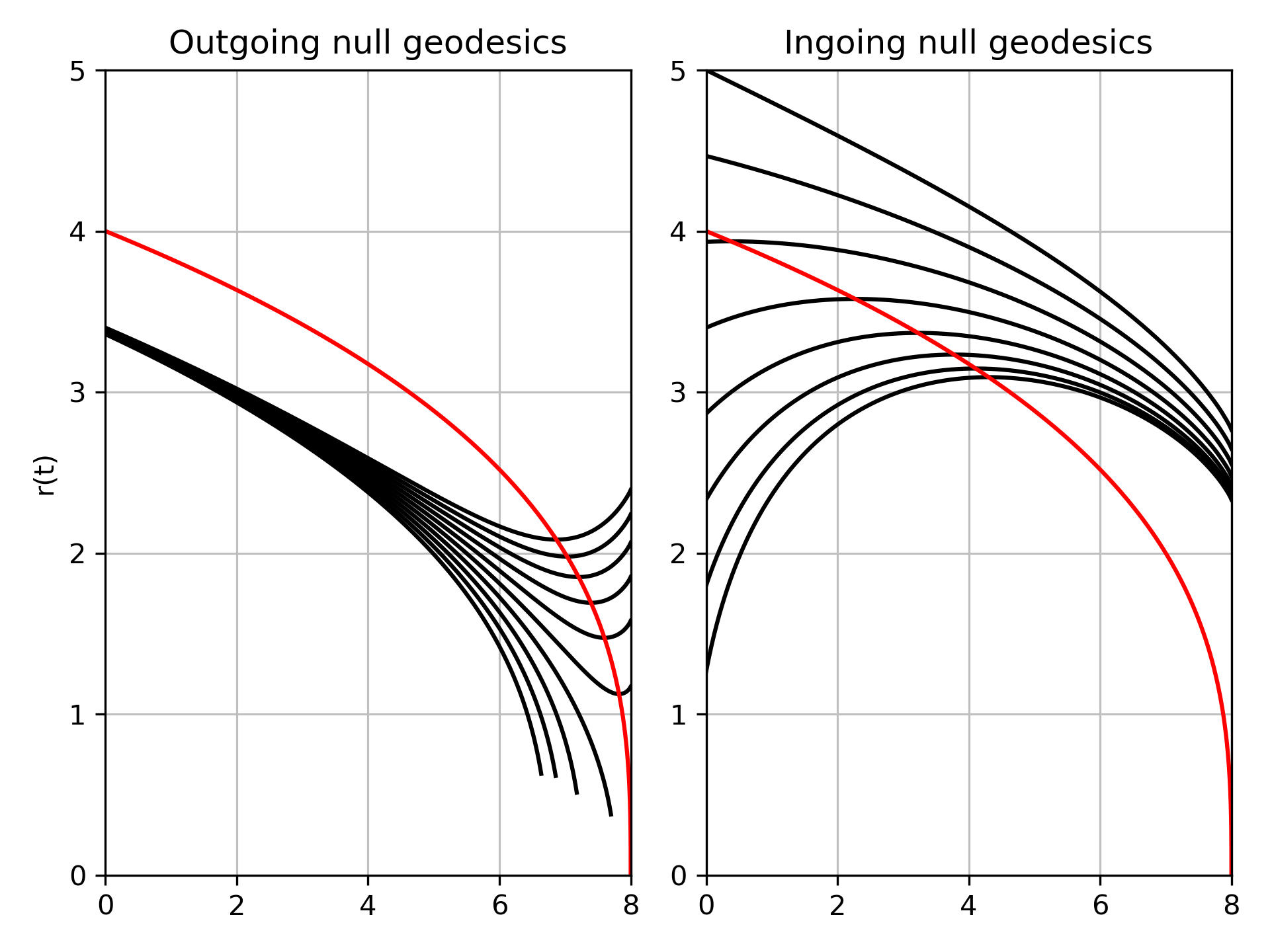
Well, I got the numerical solutions to work but it was a lot of effort. The solvers are not particularly well behaved, especially when the mass is large for some reason. One would expect that there wouldn't be too much difference as the ODE is roughly scale invariant when scaling \(m_0\) and \(r_0\) together:

\(\frac{\mathrm{d}r}{\mathrm{d}t}=\left.1-\frac{2m_0}{r}\right\vert_{t=0}\)

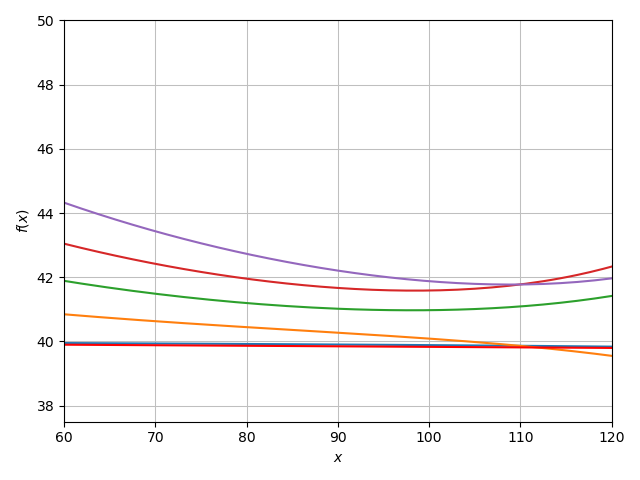
These trajectories more or less behave the way one would expect, incoming rays approach but never pass the event horizon.

A new feature that isn't ordinarily an issue, is that what we define as ingoing radiation on the exterior region appears to be outgoing on the interior. This is because coordinates for a stationary observer aren't really all that good. This does give an interesting point of view on null geodesics being trapped at the event horizon. To the Schwarzschild observer, a photon going towards the event horizon from the exterior may move inside, perhaps by quantum tunneling, but now it's on the interior where time is spacelike and the radial coordinate is timelike, so now it appears to move out towards the event horizon, where it may then tunnel out. So the ray sort of dances around the event horizon, but ultimately can't escape it.

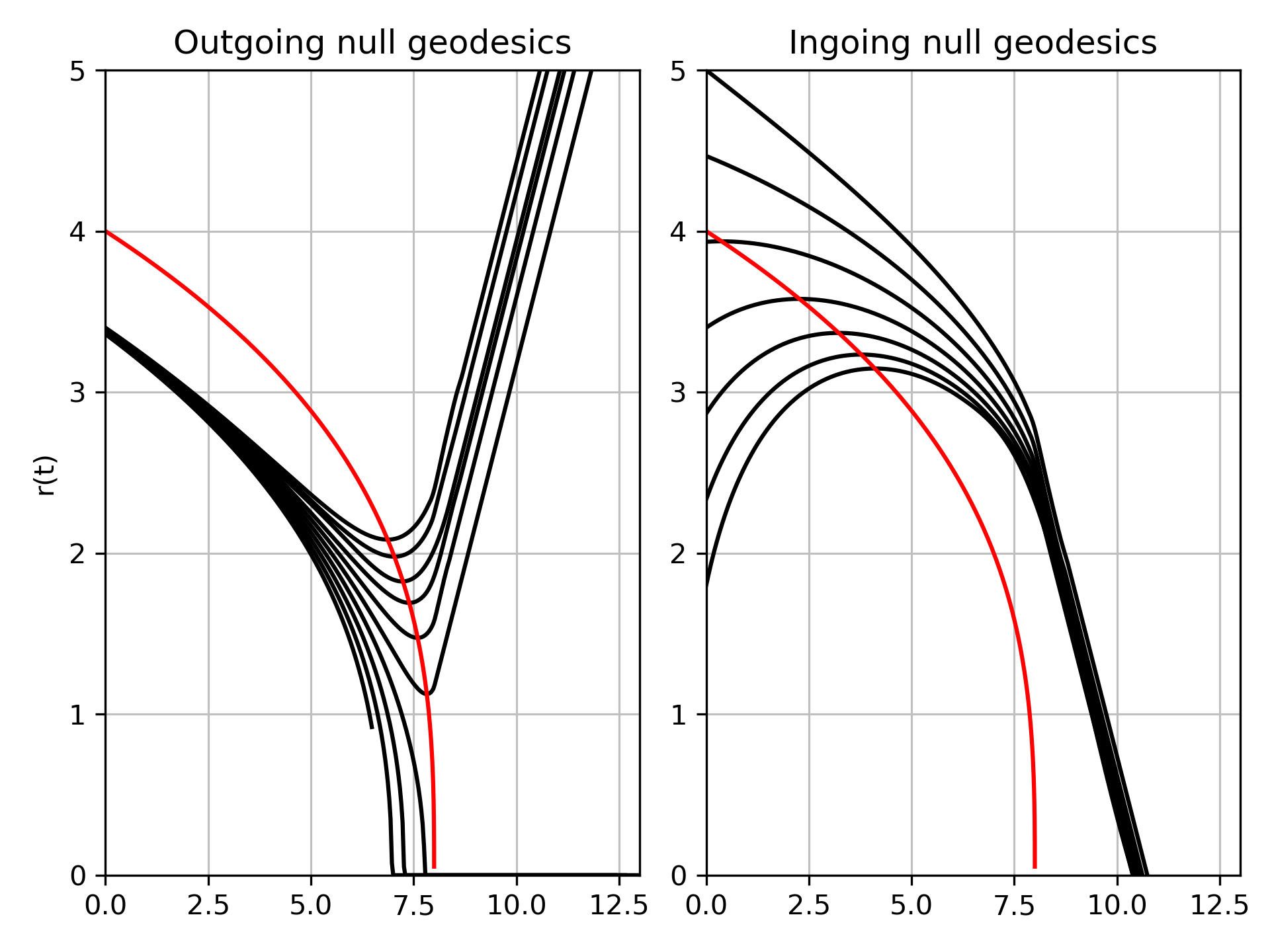
For the evaporating case, where the null geodesics can classically escape the event horizon, they "asymptotically" (not quite, but only because the horizon is moving) approach the event horizon. So it appears to a stationary observer that the horizon collapses past infalling radiation which then remains trapped close to it. This would result in a sphere of radiation that appears trapped and frozen in time (it would necessarily be invisible due to the fact that it is moving towards the horizon).

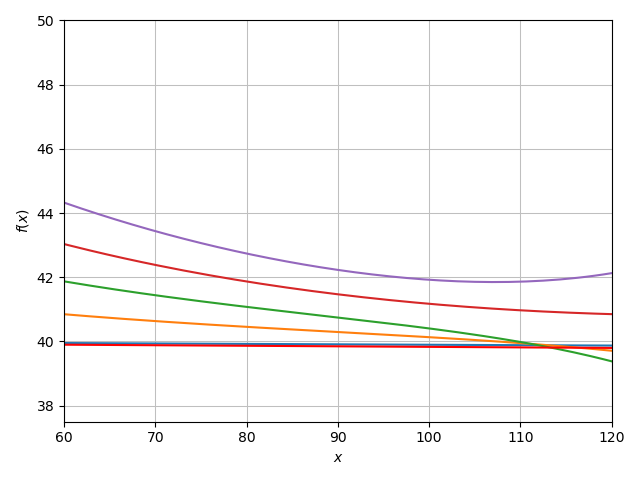
Solutions continued after the mass finishes evaporating.

In this plot, (which looks a little wonky, but works regardless) it can be seen that the Schwarzschild observer would actually see all this trapped radiation escape when the mass all evaporates.

Presumably this model is completely invalid in the \(m\approx0\) regime due to quantum effects anyway.

The other thing that would probably invalidate this, is that the Schwarzschild observer always sees all of the infalling matter that made the black hole appear to be trapped outside the horizon, and frozen in time. So nothing would be in the interior to escape in the first place. Though I am unsure how the fact that the horizon is an apparent horizon during the collapse changes this. Perhaps the fact that it grows past the collapsing star means they would actually see things fully dissapear behind the horizon, rather than just being redshifted. I'll need to read up on this a bit more.