04 - Tuesday

I've spent an awful lot of time investigating a consistent treatment of trajectories, and I have two very shaky conclusions.

1. Schwarzschild coordinates should probably not be used. They have weird and inconsistent behavior inside the horizon when comparing to other coordinate systems.
2. The sign flip probably doesn't make a whole lot of sense when crossing the horizon in Schwarzschild coordinates. The caveat here is that it probably doesn't make sense because Schwarzschild coordinates shouldn't be used in the first place. I'm basing this conclusion on the following observations. 

Take a photon that starts inside the horizon, moves outward and crosses the horizon and transform the trajectory to raindrop coordinates. 

If you don't include the sign flip, then you get the following diagrams:

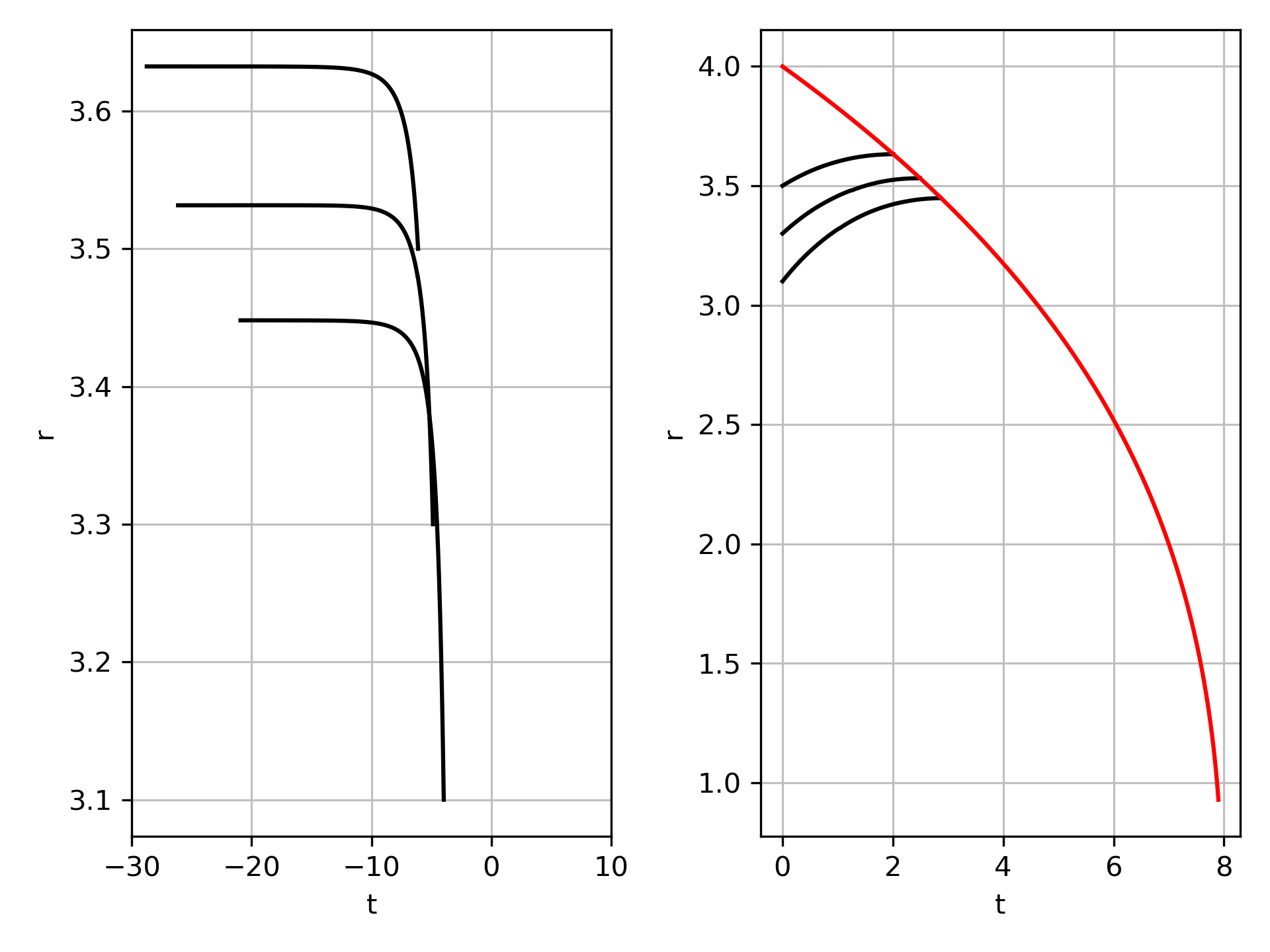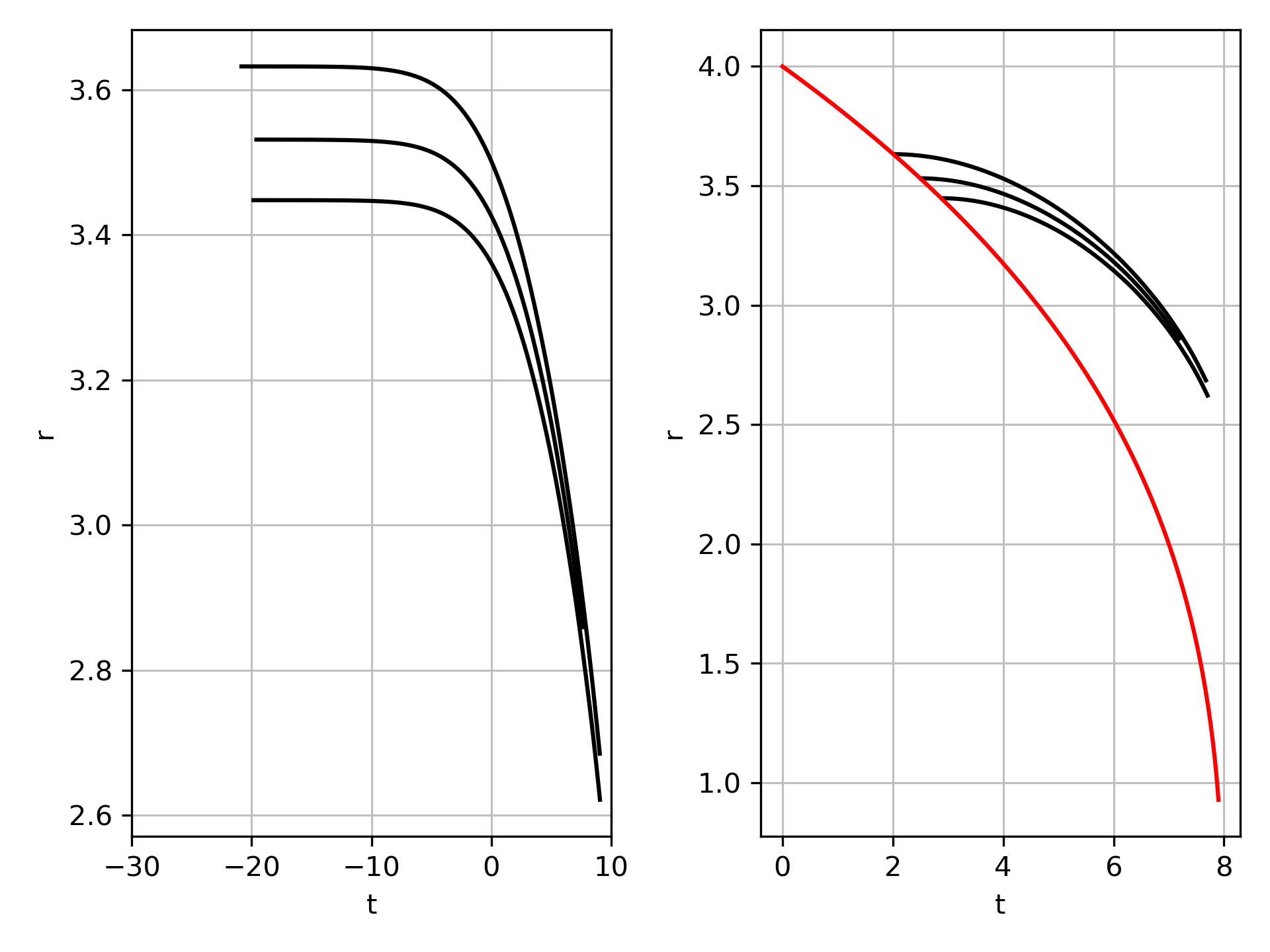The leftmost plots show the trajectory when the particles are inside the horizon according to Schwarzschild coordinates. The plots with horizons (red) are in Schwarzschild coordinates. The right most shows the trajectory when the particles are outside the Schwarzschild horizon.

Looking at the raindrop coordinates, we see two particles at the same times, both falling, so the trajectory direction is consistent, even if the number of observed photons isn't. (We see the same doubling when going from a single raindrop particle to Schwarzschild, it is exclusively a feature of the transform to/from Schwarzschild coordinates)

If one then performs the same calculations with the sign flip:

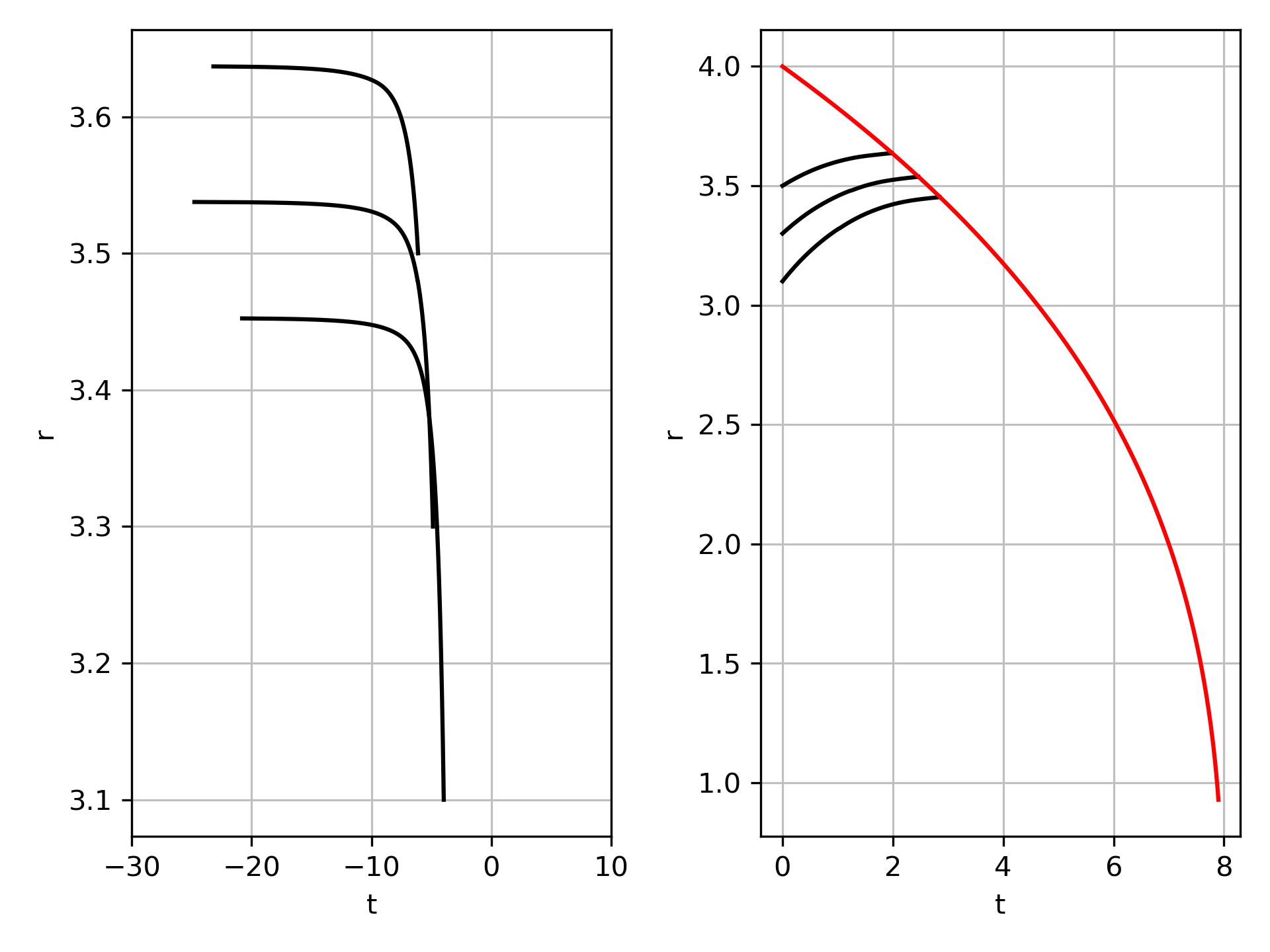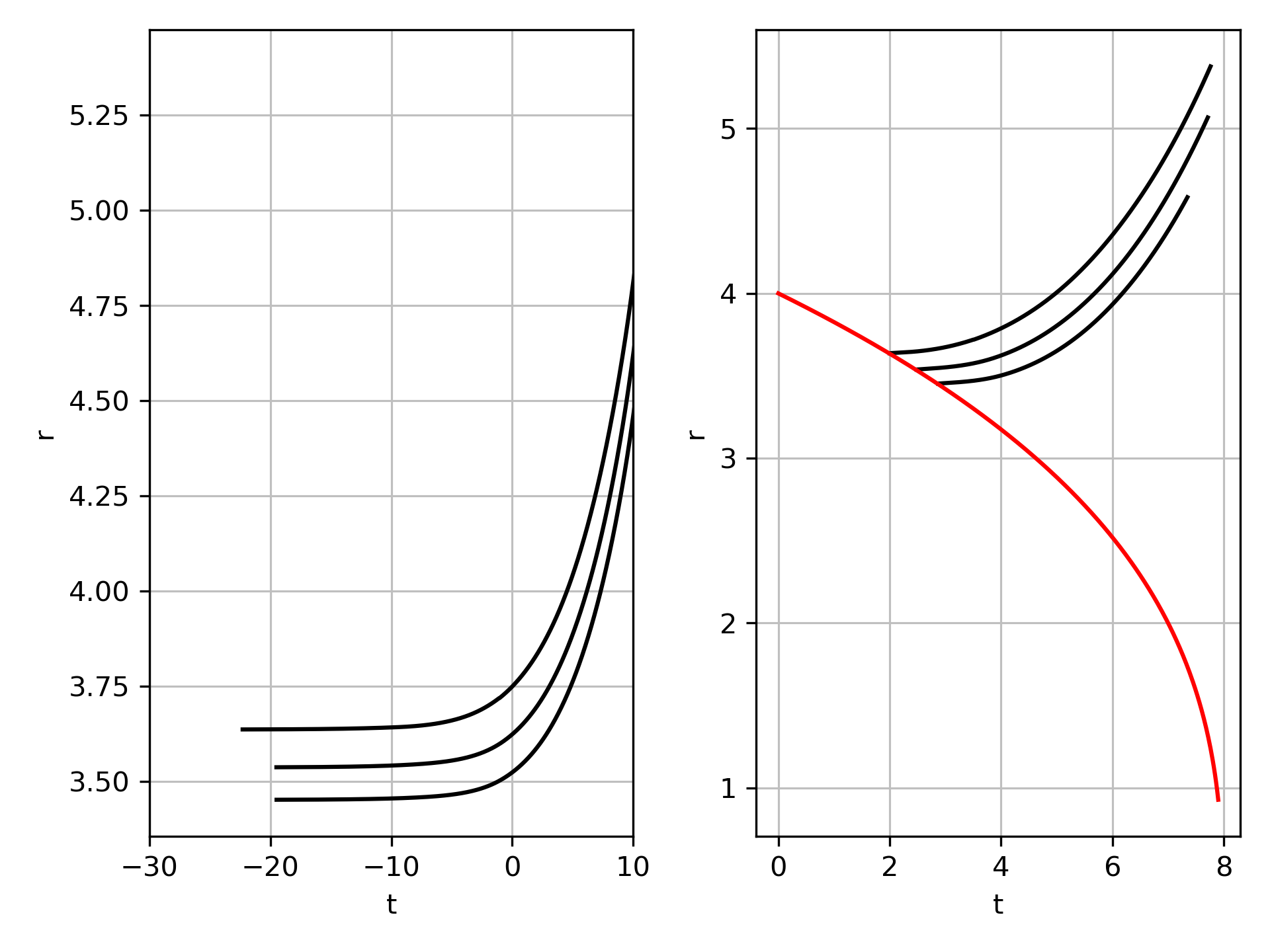We again see two photons at the same time, but the direction is inconsistent across the horizon, suggesting the sign flip might not be physically accurate. 

 

It is also worth noting that in both cases, the raindrop observer is seeing a particle that appears to drop down from the radial distance at which the photon meets the horizon and into the singularity, and one which escapes. I expect that if we were able to continue the plots in the raindrop analytically, we would see the “two” photons start at an infinite time in the past and separate at the appropriate time of evaporation. This isn't a feature one expects in raindrop coordinates, photons shouldn't ever sit still and they shouldn't appear to be stuck at the horizon. Those are features of the Schwarzschild coordinates.

The issue with basing a decision to not flip the sign on this, is that the inside trajectories in raindrop coordinates can be thought of as some sort of time reverse of an escaping particle, again we see something like this when going from raindrop to Schwarzschild coords, it is a property of the transform.