03 - Saturday

It's been a while since I've written a proper research entry. Over the past few weeks, the semester has wrapped up and I've taken some time off, I finished a long essay discussing QFT in curved spacetime in the context of Hawking radiation, gave my progress talk to the research group and started working on another research project in my spare time. 

The new project is inspired by the work of Ralph, Chang 2020 which constructs a rotating version of an Alcubierre metric on a spinning platform. In this metric, the platform itself is analogous to the Alcubierre bubble and rotating in space at arbitrary rate.

\[\mathrm{d}s^2=-(1-\omega^2r^2F^2)\mathrm{d}t^2+2\omega r^2F\mathrm{d}\phi\mathrm{d}t+\mathrm{d}r^2+\mathrm{d}z^2+r^2\mathrm{d}\phi^2\]

\(F\) is a shape function which acts to control the radius and height of the disk, the details aren't too important other than that it is a function of \(z\) and \(r\). My current preferred description of this metric is a piece of hockey puck shaped spacetime rotating about the \(z\) axis with angular velocity \(\omega\). This is almost the Born coordinate chart, except we've made a replacement \(\omega\rightarrow\omega F\). I'm careful to introduce this replacement on \(\omega\) and not \(\phi\) as that would not obtain the above metric. It does however suggest that Eulerian observers have a four velocity given by:

\[u^{\mu}=(1,0,0,-\omega F)\]

If this is the case, then we can use them to study the relationships between observers at different locations by observing that they all advance through time at the same rate (I expect \(\mathrm{d}t=\mathrm{d}\tau\) but haven't validated this yet), and so we can foliate the space into spacelike hypersurfaces defined by \(\mathrm{d}t=0\):

\[\mathrm{d}l^2=\mathrm{d}r^2+\mathrm{d}z^2+r^2\mathrm{d}\phi^2\]

(This is the line element for the induced metric on the foliation.)

Which allows a suitable definition of spacelike distances at a constant coordinate time. This lets us calculate relative velocities and enables some extremely approximate insights into doppler shift and the like. This is all very nice, though we still need to validate this four velocity is tangent to a timelike geodesic, it's trivially easy to do this far from the disk, where \(F=0\) but not so nice to compute in general. However, we can set \(F=1\) and we obtain the Born coordinate chart (which is valid for those sufficiently far inside the disk), for which the above four velocity should be valid, as it is obtained by a simple change of variables from the usual static cylindrical coordinates in flat spacetime.

Another interesting thing to look at will be the energy density of this solution, I'm expecting overall negative energy densities but I don't really have much intuition about this sort of thing. It may be worth spending some time looking at the Kerr metric to try and build up that intuition, but I can't spend too much time on this project as I need to continue working on my actual Honours project.

 

I did end up working on my honours project a little today, I'm still trying to work out how these entanglement relations work in the papers Josh sent me. It looks like a lot of that work is based on taking the Minkowski vacuum and breaking it up using light cones in each Rindler wedge. The Kruskal case is likely similar, but I really don't understand it well so far.

I also rebuilt my jupyer container so I could make use of a package designed for GR calculations, and I produced this plot of the energy density of the above metric with \(H=1, R=10, \sigma_z=\sigma_r=10, z=0, \omega=0.5\)

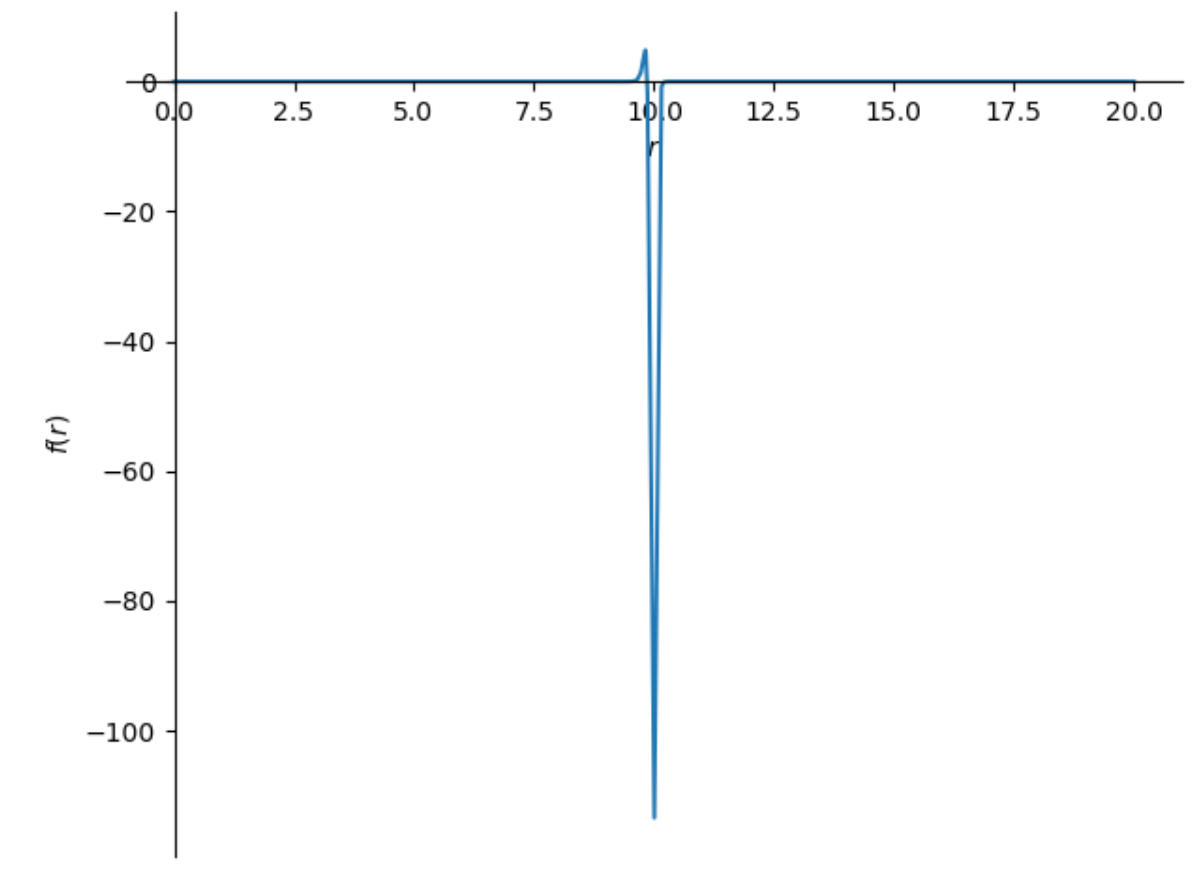
As you can see, there is a very small positive energy density inside the ring, followed by a much high negative density region. So the weak energy condition is definitely violated, though I'm not certain I expect the dominant condition is also violated.

 

 

 

 

 

 

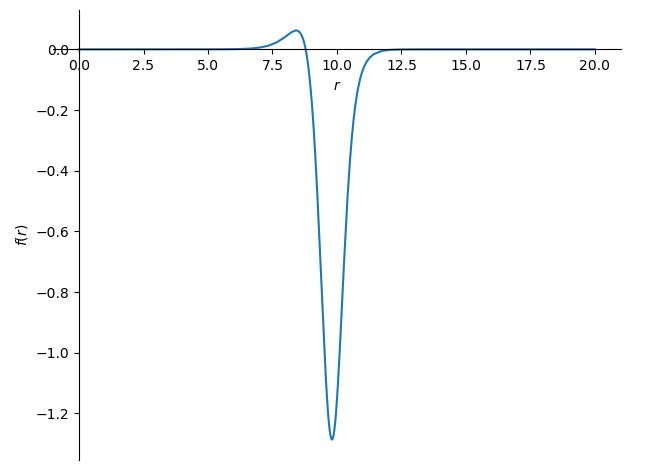
Things start looking a lot more sensible when I set \(\sigma_z=\sigma_r=1\) I also set \(H=5\) just to make sure the \(z\) part of the shape function was still roughly 1 inside the disk.

 

 

 

 

 

 

 

Taking the same parameters as the second plot, but changing the rotation rate to \(\omega=0.05\) produces this. I think this should be a disk spinning subluminally, about 0.5c at the edge.